During your schooling, were you ever faced with one of those ‘two trains left a station…’ type of maths problem? I remember finding them absolutely frustrating.

Algebra was never my thing, and I never got the point of being able to figure out when or where two trains’ paths might cross. It was altogether too much effort. They would cross sometime. When exactly mattered to no one – certainly not the people on the trains.
However, it seems that maths teachers love these formulations, and thus they keep inflicting them upon successive generations.
I have always imagined that this sort of problem was created by some harassed teacher trying to find a way to engage their wayward charges and realising that the children were infatuated with trains.
Suddenly, courtesy of the train problem, these young people all get the point of maths and go on to become algebra professors. Or not.
Strangely, I can’t find any history of the train problem to tell me whether this guess is factual. In his 1875 “A Graphic Method of Solving Certain Algebraic Problems,” George L. Vose notes that such problems had been around since at least 1850, but does not name an originator.
Still, this proves that train problems have been plaguing school children for over 170 years.
Train problems have plagued students for over 170 years — and they’re still missing the point.
If my guess is correct, the original children who received these problems probably did fall upon them hungrily, happy to be dealing with something tangible amidst the forest of disconnected algebraic a’s b’s and x’s.
And that is the point. In a class full of train-mad children at the beginnings of the steam age, such a problem may have been a most effective teaching tool.
Disconnected from this context, however, it has become a stock item to be received with a resigned sigh.
I first understood how important context was in education when I was a student teacher. As part of my practical experience I spent some weeks observing an inspirational teacher called Sherida Walters. She did some wonderful lessons, and I was inspired by her approach.
So, when I got my own class, and was wanting to get off to a strong start, I tried to replicate some of these lessons. Abject failure.
Initially it made no sense, but on reflection, I realised that a teaching approach cannot be disconnected from the teacher. What works for one teacher may not work for another. It all depends on the context – what the teacher brings to the table in terms of temperament and enthusiasm, and also what the class needs on that particular day.
The perfect learning moment is not static and cannot be passed on in formulae. It is a dynamic thing that needs to be recaptured each time a teacher steps into a classroom.
Teaching, in other words, is an art, not a science.
The perfect learning moment isn’t fixed — it must be recaptured every time a teacher walks into the room.
And this is why formulae like the train problem end up becoming boring. They may have been a unique and brilliant solution to a specific problem somewhere around 1850 but, to be effective today, they have to be properly reinvented – and not just by changing the names of the stations to somewhere nearby.
In researching the history of this problem, though, I did come across one version I really liked. If one man left Las Vegas driving at 80 miles per hour, and another left Los Angeles travelling at 75mph, where would they meet?
The answer someone came up with was jail, because the speed limit was 55! That is a person attuned to context.


Each vignette invites readers to embrace the beauty of unfinished thinking and the art of holding life’s ongoing questions.


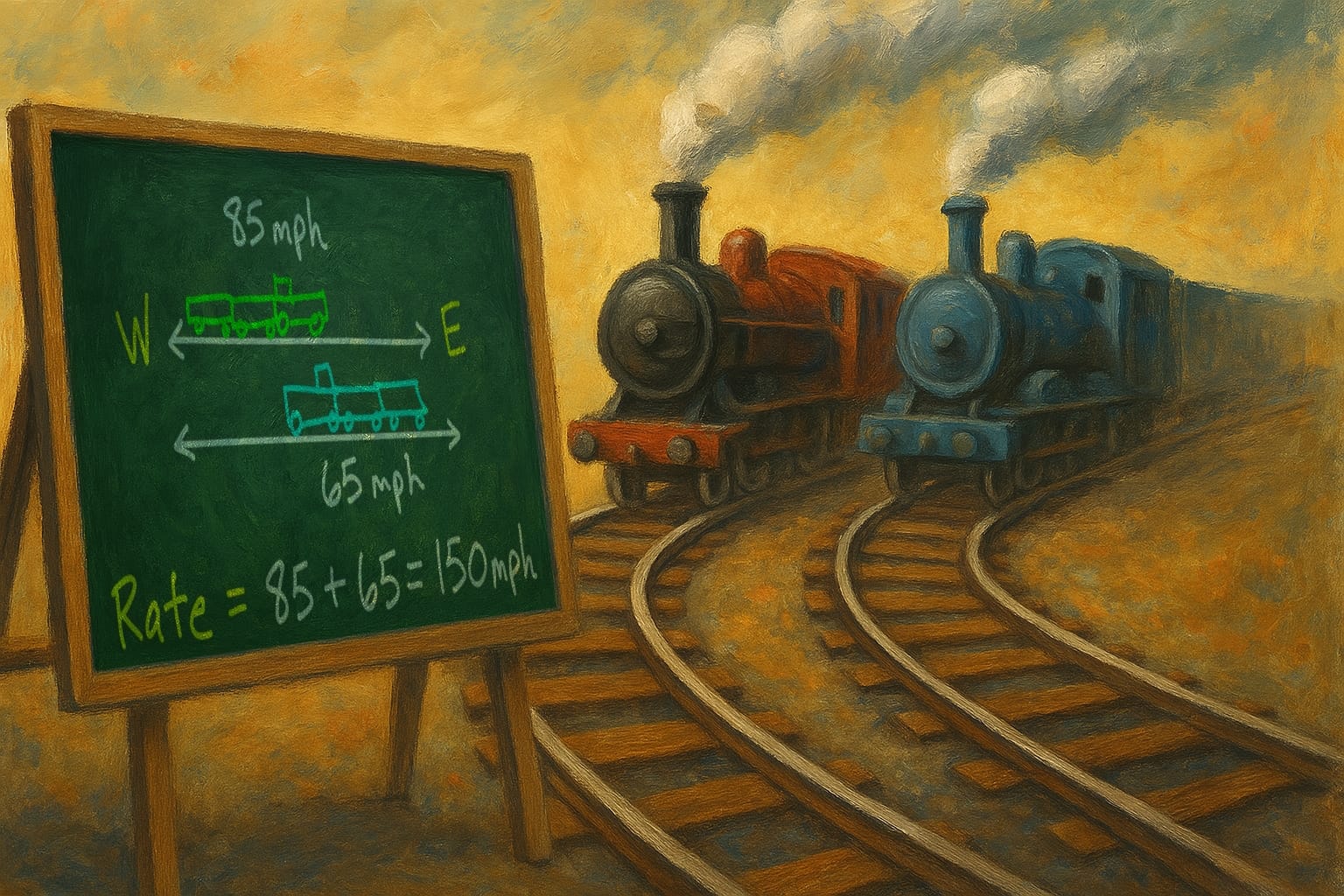








Member discussion